- Consider the solution OPT
- How do we make OPT more like our solution?
- Do this without making OPT worse!
- The greedy algorithm sorts the values
- Sorting hints towards proving this by considering inversions
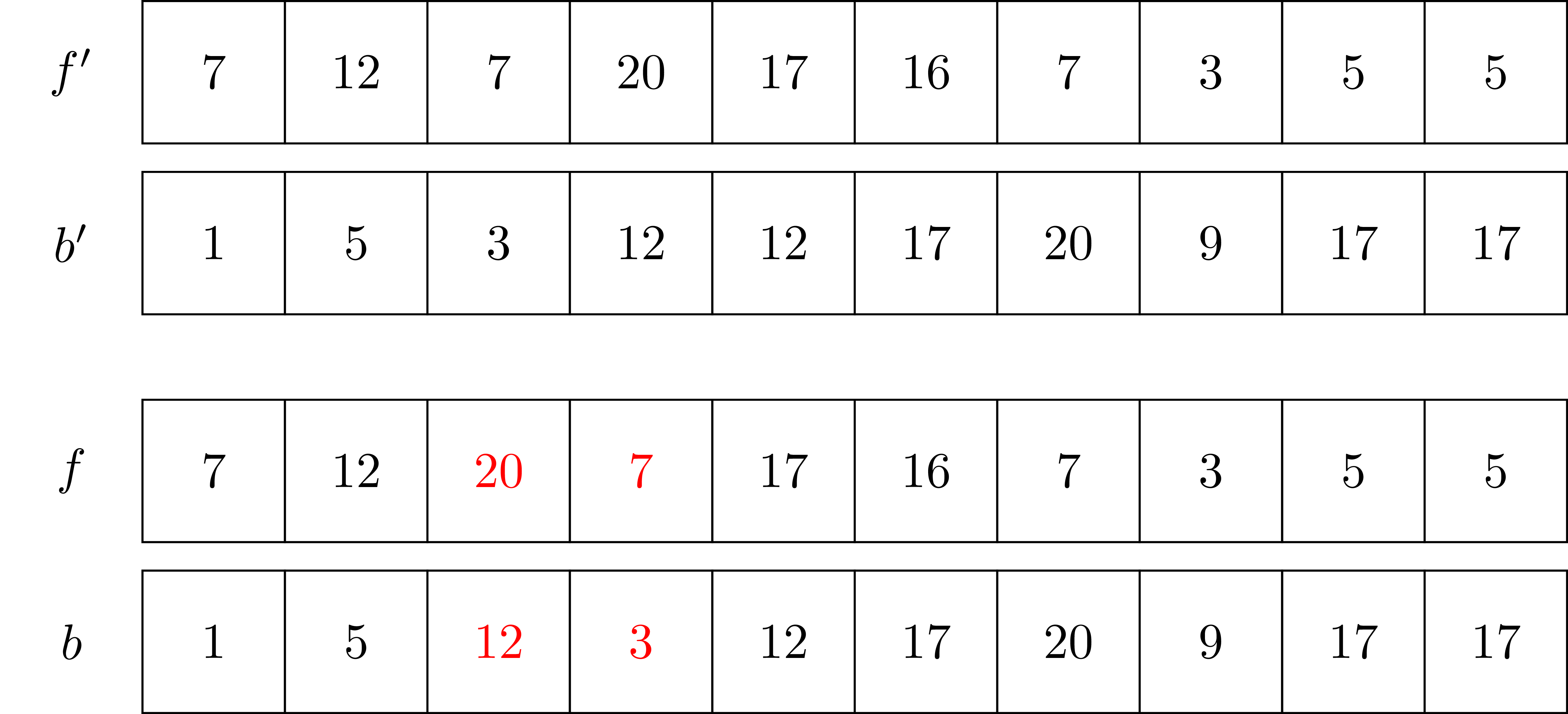
- Find some
- Example:
- Show that the swap only ever improves the solution!
- Reminiscent of the Pizza Baking Time Problem
- Example:
- Calculate the contribution to the weighted sum for the
- Let
- Pizza
- Pizza
- Total Contribution:
- Let
- Then consider what happens after the swap
- Pizza
- Pizza
- Total Contribution:
- Pizza
- Left hand side is the contribution after the swap
- If
- Recall that
- Comparing inversions which are not consecutive
- This causes all contributions between
- This causes all contributions between
- Assuming the inversion is only at the first index
- Isolating the variables
- Unnecessarily attempting to prove using induction
- While technically correct, this bogs us down in details
- Not proving it!
- Stating that it is worse is not sufficient
- Vector
- Goal: Find the missing integer in
- Constraint: May only access elements using
bit[i, j]- Returns the
- Returns the
- The Usual Suspects for D & C
- Split the array directly in half
- Sort elements then split in half
- Neither of these usual suspects will get us anywhere
- We must look deeper at the properties we have
- We are looking at the bit representation of
- Let us look at a small example:
| Number | Binary | Number | Binary |
|---|---|---|---|
| 0 | 000 | 4 | 100 |
| 1 | 001 | 5 | 101 |
| 2 | 010 | 6 | 110 |
| 3 | 011 | 7 | 111 |
- Group all of the numbers with
- Do the same for
- Do the same for
- Whichever group is smaller is missing their bit at
- Recurse into the smaller group to get the rest of the bits
- Master theorem!
- Defaulting to one of the usual suspects
- Good instinct to try, but this strategy would ultimately not work out
- Binary search is too fast!
- Assuming the array is sorted
- There is a
- Problem statement did not specify
- Sorting takes
- There is a
- Secretly using the
bitoperation- If you got the value of an integer, that took
- If you compared two integers to each other, that took
- If you got the value of an integer, that took