Overview

• Greedy algorithms make a series of choices, each locally optimal, to reach a global solution.
• Efficient for certain types of optimization problems.

Pizza Order Scheduling

• Manage pizza orders with one chef and a galactic oven
• Making pizza involves two stages: preparation and baking
  • Takes in stage 1 and in stage 2
  • One chef for stage 1, infinite space for stage 2
• What order should we use these pizzas?
• Goal: Minimize the time until the last pizza is baked.

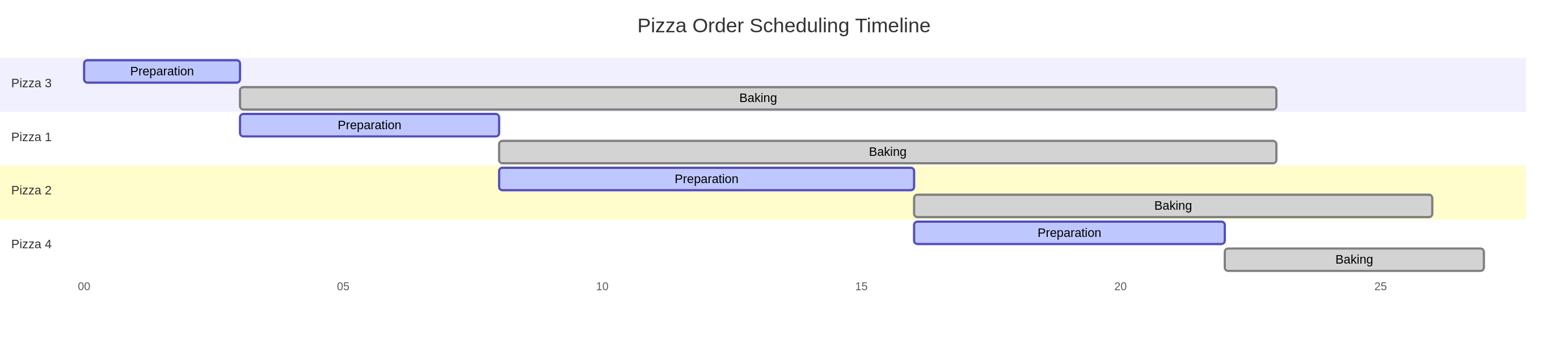
Problem Setup

Optimal Order

Solution Approach

• Each of the preparations happen one after the other
  • Does the order impact preparation time?
• What about the baking time?
• The pizza that takes the longest to bake should be put in first

Greedy Solution

• Sort orders by non-increasing baking time
• This ensures the pizzas with the longest baking times go into the oven first

Proof of Optimality

• Consider any non-optimal permutation.
  • Identify consecutive pizzas and
  • Current order: then where

Proof of Optimality

• Case Analysis:

  • Pizza Finish Time :
  • Pizza Finish Time :

• What If We Swap?:

  • Pizza Finish Time :
  • Pizza Finish Time :

Cache Eviction Scheduling

• Cache holds data pieces, where is the total memory
  • We can store some data into the cache, which is fast
  • If we want to store data, but the cache is full, we have to evict something
  • aka Cache Miss
• Suppose we have a sequence of requests
• We would like to minimize cache misses

Farthest-in-Future Eviction Strategy

• Policy: Evict the data item needed farthest in the future
• Intuition: Keeps most immediately needed items in cache
• Not realistically possible, but pretend we have such a machine
• Goal: Show this is the best we can do to minimize cache misses

Reduced Schedules

• Definition: Reduced schedule performs evictions only on cache misses
• Prove the following:
  • For any non-reduced schedule , there’s a reduced with
    the same or fewer evictions

Reduced Schedules

• Proof is very simple!
• Instead of evicting without a cache miss, just wait until there is one!
• No negative impacts on procrastinating

Proving Optimality of Farthest-in-Future

• Suppose we have i.e. schedule for farthest in future eviction
• Consider some schedule with the fewest cache misses
• Prove that any can be converted into without more cache misses

Proving Optimality of Farthest-in-Future

• Let us consider a conversion
• We show:
  1. will have the same cache contents as
  2. and have the same number of evictions

Proving Optimality of Farthest-in-Future

• Proof is through induction, suppose the statement holds for
  • At the eviction between and may differ
  • Suppose is being requested and and are evicted
  • Have evict instead of
  • Now they are the same, but does still have the same cache misses?
  • Look at the next time they differ: both instances can be resolved