Proving NP-Completeness

• Various properties exist for NP-Completeness

• Verifying a solution in polynomial time (NP)
• Show it is at least as hard as some other NP-Complete problem (NP-Hard)

Dominating Set

• A subset of the verticies in a graph such that every vertex is either in or is adjacent to it
• Find a dominating set of size
• Is this problem NP-Complete?

Example Graph

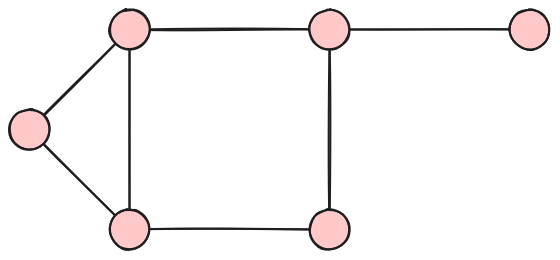
Example Graph

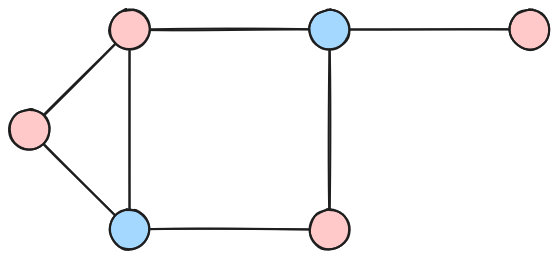
Dominating Set is NP

• Given a set of vertices
• Check for every vertex in the original graph if it is in
• If it is not, check each of its neighbors
• Time Complexity:

Dominating Set is NP-Hard

• Use the unknown to solve the known!
  • Unknown: Dominating Set
  • Known: ... ?
• Identifying the problem which performs the best reduction
• Takes experience to be able to do so effectively
• An attempt for the thought process you may have

What Problems Are Related?

• Graph Problems
  • Independent Set
  • Vertex Cover
  • 3 Coloring
• Other Problems
  • Set Cover
• Are we minimizing or maximizing in dominating set?
  • Minimizing!
  • Not a hard and fast rule, but perhaps a hint

Dominating Set -> Independent Set

• Getting rid of the additional vertex may be tricky
• Potentially dealing with cliques
• Overall getting messy

Dominating Set -> Vertex Cover

• Optimizations are aligned
• Recall for every edge, an adjacent vertex must be in the cover
• What if we made the edges vertices as well?

Dominating Set -> Vertex Cover

• Process:
  • For every edge add a new vertex called
  • Connect this new vertex to vertices and
  • Find a dominating set of size

Dominating Set -> Vertex Cover

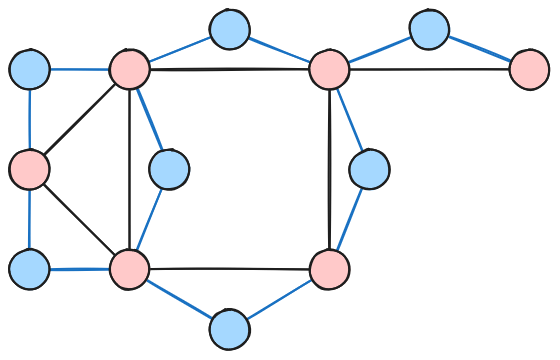
Dominating Set -> Vertex Cover

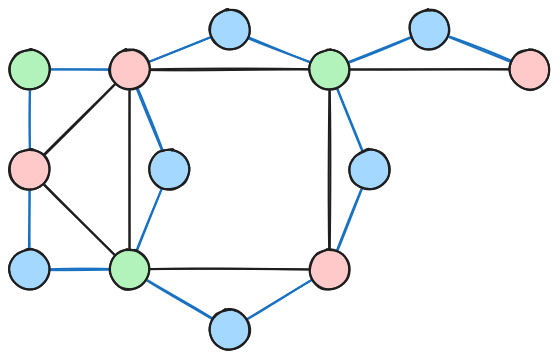
Algorithm Will Find Vertex Cover

• Let us decipher the output of the algorithm
  • Dominating set picks a set of vertices adjacent to all other vertices
  • Edges now have a vertex representitive
  • All edges are either adjacent to a vertex or "they" were picked
• Some intuition, but now we must prove it

No False Positives

• Prove: The algorithm finds a valid vertex cover of size
• For each "edge" picked, pick either adjacent vertex
• For every edge in the graph, there must be either or in the picked set

No False Negatives

• Prove: If there is a vertex cover of size a dominating set of size must also exist
• Take the vertex cover of the initial graph of size
• In the corresponding modified graph, it is also a dominating set
• Every vertex cover is also a dominating set
• Adding the extra edges does not affect the domination in any way

0-1 Knapsack

• A backpack can carry weight
• There is set of items to take
• Each item has a weight and benefit value
• Goal: select a subset of the items such that
  • Total weight is at most
  • Maximizing total benefit of the items

Isn't That Strange?

• But we have a solution of ?
• This actually doesn't count because of the
• can actually be massive and completely screw up the time complexity

0-1 Knapsack is NP

• Is this true?
• No
  • How do we know that this is actually the largest?
• We can modify this to be
  • Is there a set of items that have a benefit of and under ?
• Now is this NP?

0-1 Knapsack is NP-Hard

• Use the unknown to solve the known
  • Unknown: 0-1 Knapsack
  • Known: Subset Sum
• This one is a bit obvious, hopefully?

0-1 Knapsack -> Subset Sum

• How should we solve Subset Sum with 0-1 Knapsack?
• Take each number in Subset Sum, convert to item
  • Benefit: number
  • Weight: 1
• Set the max weight to be the total number of elements (or )
• Set benefit target as the target from Subset Sum

Proof

• Hopefully the proof is intuitive, but we do need to go through the motions
• No False Positives: Summation of elements is which is the target for Subset Sum
• No False Negatives: Solution for Subset Sum would work for Knapsack

Clustering Problem

• Given a weighted graph an integer and a target divide the vertices into sets
  • Any pair of nodes in the same set should have a shortest path length of
• Is this problem NP-Complete?

Clustering is in NP

• Given an assignment of clusters
• Make sure there are of them
• For every pair of vertices in a cluster, verify the shortest path is at most
  • How many pairs of vertices are there?
  • Upper bound on ?
• Takes at most

Clustering is NP-Hard

• Use the unknown to solve the known!
  • Unknown: Clustering
  • Known: ... ?
• Another attempt at some problem solving

What Problems Are Related?

• Graph Problems
  • Independent Set
  • Vertex Cover
  • Dominating Set
  • 3 Coloring
• Other Problems
  • Set Cover
  • Subset Sum

Some Thought Processes

• Independent Set, Vertex Cover, Dominating Set
  • All structurally similar, but the value is hard to translate
• Let's look at 3-Coloring instead

Some Thought Process

• We know that 3-Coloring is grouping vertices into 3 sets
• Trying to find a valid grouping, similar to clustering
• would be
• How would the weights factor in?
• Use the weights as a way to keep the adjacent nodes in separate sets

Clustering -> 3-Color

• Create a new weighted graph with the same vertices, but is a complete graph
• All edges in the original graph have a weight of 2
• All other edges have a weight of 1
• Set and

Deciphering the Output

• Every adjacent node has a weight of 2, automatically exceeding the target
• Any alternate path will also be at least 2
• Prevents adjacent nodes from being in the same cluster
• Now we must prove that this holds

No False Positives

• Suppose there is a cluster that does not translate to a coloring
• Means there are two adjacent nodes in the same clustering
• But this is impossible, as the shortest distance must be 2
• Contradiction!

No False Negatives

• Suppose there is a 3 coloring that does not translate to a clustering
• Means 2 vertices have the same color, but shortest distance is 2
• Same color means non adjacent
• Graph is set up to create an edge of weight 1 if they are not adjacent
• Contradiction!