Problem Example
- Solution:
Recursive Solution
- We have 2 inputs we can modify:
- We will ignore
- We will ignore
- A smaller problem is either smaller
- We can more reliably shrink
Recursive Solution
- How should we get rid of an element?
- Make a decision with the element
- Now that we have a smaller problem, what do we do?
- Make a recursive call!
Recursive Solution
def KnapSack(S, W, n):
# Base Case
if False:
pass
# Recursive Step
include = KnapSack(S, ?, n - 1) + S[0].b
not_include = KnapSack(S, ?, n - 1)
return None # Not done yet
Recursive Solution
def KnapSack(S, W, n):
# Base Case
if False:
pass
# Recursive Step
include = KnapSack(S, W - S[n - 1].w, n - 1) + S[0].b
not_include = KnapSack(S, W, n - 1)
return None # Not done yet
Recursive Solution
def KnapSack(S, W, n):
# Base Case
if False:
pass
# Recursive Step
include = KnapSack(S, W - S[n - 1].w, n - 1) + S[0].b
not_include = KnapSack(S, W, n - 1)
return max(include, not_include)
Recursive Solution
def KnapSack(S, W, n):
# Base Case
if W == 0 or n == 0:
return 0
if S[0].w > W:
return KnapSack(S, W, n - 1)
# Recursive Step
include = KnapSack(S, W - S[n - 1].w, n - 1) + S[0].b
not_include = KnapSack(S, W, n - 1)
return max(include, not_include)
Memoization Solution
- Which values are changing in the KnapSack problem?
- What is a major problem with our current solution?
- Redoing calculations!
- Same input = Same output!
- We want to have a table keep track of calculations we already did!
Memoization Solution
- What is the range of
- Smallest: 0
- Largest:
- What is the range of
- Smallest: 0
- Largest:
- A table of size
Memoization Solution
memo = Matrix(W, n)
def KnapSack(S, W, n):
# Base Case
if W == 0 or n == 0:
return 0
if S[0].w > W:
return KnapSack(S, W, n - 1)
# Recursive Step
include = KnapSack(S, W - S[n - 1].w, n - 1) + S[0].b
not_include = KnapSack(S, W, n - 1)
return max(include, not_include)
Memoization Solution
memo = Matrix(W, n)
def KnapSack(S, W, n):
# Base Case
if W == 0 or n == 0:
return 0
if memo[W][n] != None:
return memo[W][n]
if S[0].w > W:
return KnapSack(S, W, n - 1)
# Recursive Step
include = KnapSack(S, W - S[n - 1].w, n - 1) + S[0].b
not_include = KnapSack(S, W, n - 1)
return max(include, not_include)
Memoization Solution
memo = Matrix(W, n)
def KnapSack(S, W, n):
# Base Case
if W == 0 or n == 0:
return 0
if memo[W][n] != None:
return memo[W][n]
if S[0].w > W:
return memo[W][n] := KnapSack(S, W, n - 1)
# Recursive Step
include = KnapSack(S, W - S[n - 1].w, n - 1) + S[0].b
not_include = KnapSack(S, W, n - 1)
return memo[W][n] := max(include, not_include)
Backtracking Solution
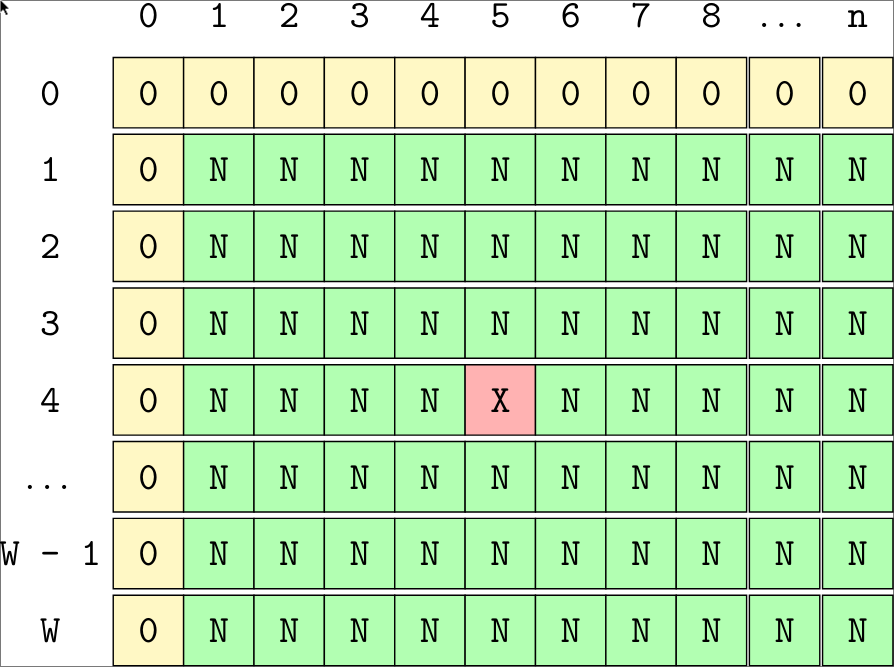
Backtracking Solution
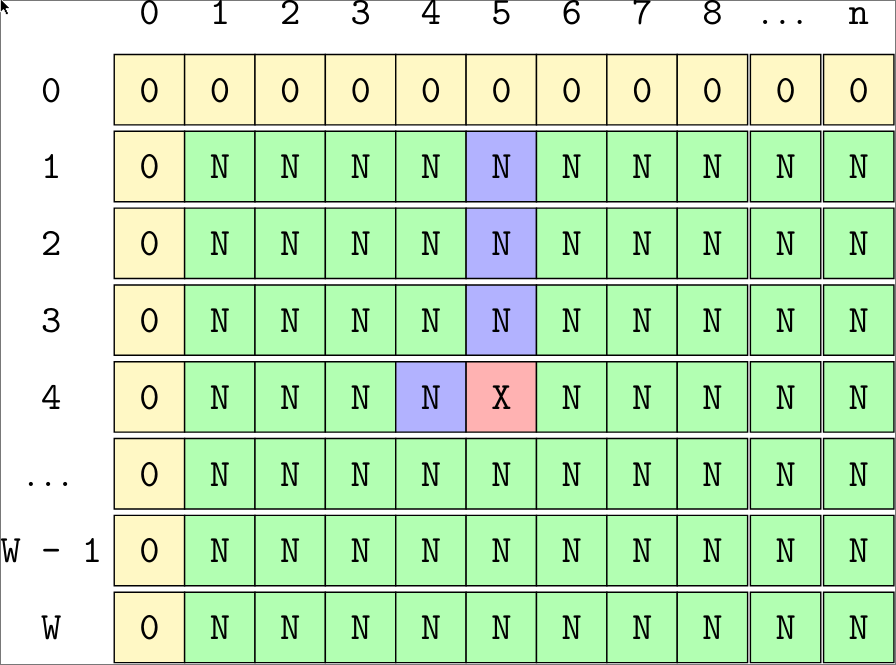
Backtracking Solution
def KnapSack(S, W, N):
memo = Matrix(W, n)
for n in range(1, N + 1):
for w in range(1, W + 1):
pass
Backtracking Solution
def KnapSack(S, W, N):
memo = Matrix(W, n)
for n in range(1, N + 1):
for w in range(1, W + 1):
if S[n].w > W:
memo[w][n] = memo[W][n - 1]
else:
include = memo[w - S[n - 1].w][n - 1] + S[n - 1].b
not_include = memo[w][n - 1]
memo[w][n] = max(include, not_include)
return memo[N][W]
Homework Assignment
- There are two homework types: easy and hard
- Points for homework
- Doing hard homework requires not doing the previous assignment
- What is the largest number of points you can get?
Problem Example
- Solution:
Recursive Solution
- We have 1 input we can modify:
- Similar to last time, we are ignoring the set
- Similar to last time, we are ignoring the set
- Making the problem smaller means making
- We can shrink
Recursive Solution
- How do we make this problem smaller?
- How do we then combine the solutions?
Recursive Solution
def Homework(e, h, n): # Not enough parameters!
# Base Case
if False:
pass
# Recursive Step
return None # Not done yet
Recursive Solution
def Homework(e, h, n, rested):
# Base Case
if n == 0:
return 0
# Recursive Step
nothing = Homework(e, h, n - 1, True)
easy = e[n - 1] + Homework(e, h, n - 1, False)
hard = h[n - 1] + Homework(e, h, n - 1, False) if rested else 0
return max(nothing, easy, hard) # Not done yet
Backtracking Solution
def Homework(e, h, n):
memo = Matrix(n, 2)
for i in range(n):
for rested in range(2):
nothing = memo[i - 1][1]
easy = e[n - 1] + memo[i - 1][0]
hard = h[n - 1] + memo[n - 1][0] if rested else 0